What is Hashing?
Hashing is a technique used to assign values to a key, employing various hashing algorithms. One might wonder about the purpose of hashing in NLP. Well, when you're attempting to translate one language to another, let's say Nepali to English, and you're using word embeddings for both languages, there is a need for organizing similar words before training a model to identify them. This involves placing similar words from both languages into the same list, enabling the creation of a matrix that maps embeddings from one language to their corresponding words in the other language.
To achieve this, hashing is utilized to group similar words from both languages into the same bucket based on their word embeddings. However, using traditional hashing techniques does not guarantee that similar words will be assigned to the same bucket. To address this challenge, Locality Sensitive Hashing (LSH) can be employed. LSH facilitates the determination of similarity between data points and ensures that they are mapped to the same or nearby buckets, thereby accomplishing the grouping of similar words effectively.
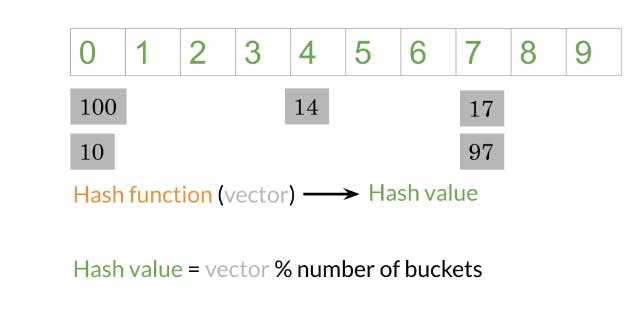
Here's a step-by-step explanation of the method:
Plane Definition: The first step is to define a plane in the space. A plane can be represented by a normal vector and a point on the plane, or by an equation that describes the plane. The normal vector indicates the direction perpendicular to the plane.
Position Calculation: For each data point, the position with respect to the plane is determined. This can be done by calculating the signed distance between the data point and the plane. The sign of the distance indicates whether the point is on one side or the other side of the plane.
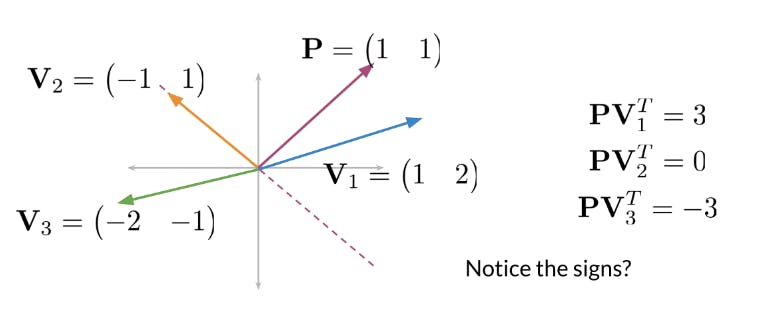
Hashing: Based on the calculated position, the data points are then hashed into buckets. Typically, a hash function is used to map the position to a hash code or bucket. Data points with similar positions or on the same side of the plane are more likely to be mapped to the same or nearby buckets.
We can use multiple planes to get a single hash value. Let's take a look at the following example: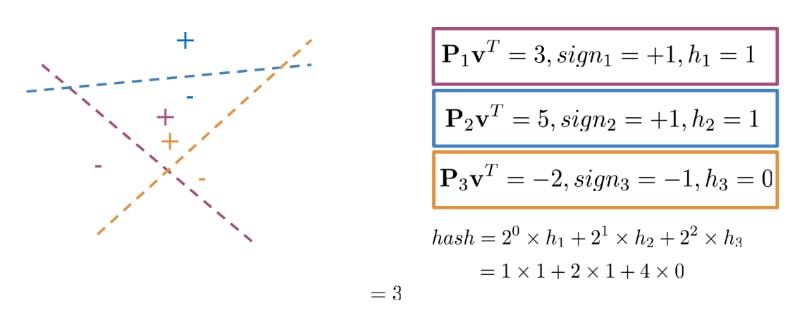
Let's consider an example to illustrate how this hashing function works. Suppose we have 3 planes, and a data point has the following positions relative to the planes: h0 = 1 (on the same side of the first plane), h1 = 1 (on the other side of the second plane), h2 = 0 (on the same side of the third plane). Using the hashing function, the hash code for this data point would be:
2^0 *1 + 2^1 *1 + 2^2 * 0 = 2 + 1 + 0 = 3
So, the data point would be hashed to bucket number 3.
The advantage of this hashing function is that it generates distinct hash codes for different combinations of positions, allowing similar data points with the same or nearby positions to be mapped to the same or nearby buckets. By adjusting the weights (powers of 2), you can control the importance of each position value in the final hash code.Indexing and Retrieval: The hashed data points are stored in a data structure, such as a hash table or hash map, where each bucket contains the data points that hashed to the same code. During retrieval, given a query data point, its position with respect to the planes is calculated, and the search is performed within the bucket(s) corresponding to the hashed position.
This method leverages the concept of separating data points based on their position relative to the plane. Points that lie on the same side of the plane are considered more similar to each other, and therefore, they are likely to be hashed into the same buckets.
It's important to note that the specific implementation and choice of hash functions may vary depending on the requirements and characteristics of the data. The design of the hash functions aims to maximize the probability of mapping similar data points to the same buckets while maintaining an acceptable level of collision (different data points being mapped to the same bucket).
This approach can be particularly useful for certain types of data and similarity search tasks where separating data points based on their position to a plane is meaningful for capturing similarity.